文章地址:tbd
标题:FedSel: ederated SGD under Local Differential Privacy with Top-k Dimension Selection
作者:Ruixuan Liu, Yang Cao, Masatoshi Yoshikawa, Hong Chen
发表会议:DASFAA 2020
- Introduction
- Preliminaries
- Federated SGD
- Local Differential Privacy
- Problem Definition
- Two-stage LDP framework: FedSel
- Overview
- Privacy Guarantee
- Variance Analysis for Accumulation
- Private Dimension Selection
- Selection Mechanisms
- Analyses of accuracy and time complexity
- Experiments
- Experimental Setup
- Evaluation of the Dimension Selection
- Effectiveness of the Two-stage Framework
- Conclusions
Introduction
第一段大概讲了一下 SGD 和 LDP 广泛应用。第二段讲了LDP方法用到SGD上面存在的噪声问题,总结大概就是如下表所示。

背景知识可以看这个博客,里面说的很清楚了:分布式机器学习:联邦学习。大概就是在联邦学习中,每个本地client需要计算梯度发送给服务器,这个梯度是 $d$ 维的,但是处于隐私保护,我们不能直接发送梯度。
然后,本文的核心点是,我们认为对于本地数据来说,并不是所有的维度都是同等重要的,我们认为绝对值大的维度对于数据传输显然更重要,所以作者提出了基于 top-k 的数据传输。总体来说,贡献点如下:
- 本文提出了一个双阶段框架:FedSel,首先经过 Dimension Selection,然后对值进行替代,即 Value Perturbation。理论分析本文的工作有着更小的error bound。(Value Perturbation实际上用的是已有的方案)
- 我们提出了不同的 Dimension Selection 方法,我们表明,对 top-k 梯度处理比已有的 top-1 的处理方法更优。
- 我们进行了大量的实验去印证实验效果。
Preliminaries
Federated SGD
假定一个learning任务定义了loss函数对于数据$(x,y)$有$L(w;x,y)$,目标是得到最优参数 $w\in\mathbb{R}^d$,使得在$N$个数据上,$w^{*}=\arg \min_{w} \frac{1}{N} \sum_{i=1}^{N} L\left(w;x_i, y_i \right)$。对于一次迭代,一个batch中 $m$ 个客户端(Client)更新本地模型并将数据发送给服务器,服务器更新全局模型:
Local Differential Privacy
差分隐私的定义如下:对于输入数据 $v,v’\in\mathcal{V}$ 和输出 $v^{* } $ 有 $\Pr[\mathcal{M}(v)=v^*]\le e^\epsilon \cdot \Pr[\mathcal{M}(v’)=v^*]$。
Problem Definition
本文研究的就是 LDP 下完成 federated SGD。在非隐私保护的场景中,梯度 $g^{t} \leftarrow \nabla L\left(w^{t-1} ; x, y\right)$ 在传输前可以被 sparsified[21] 或者 quantized[22]。不失一般性,我们用 $v_i$ 表示用户 $(x_i,y_i)$ 计算的本地梯度,然后将全局参数设为 $w^{t-1}$。
假设全局模型迭代 $E$ 次,并且对于每个 client 的 privacy budget 为 $\epsilon$,同时学习率为 $\alpha$。对于一次 epoch 来说,然后每个 batch 包含了 $m$ 个客户端。全局的模型按照以下过程迭代:
Two-stage LDP framework: FedSel
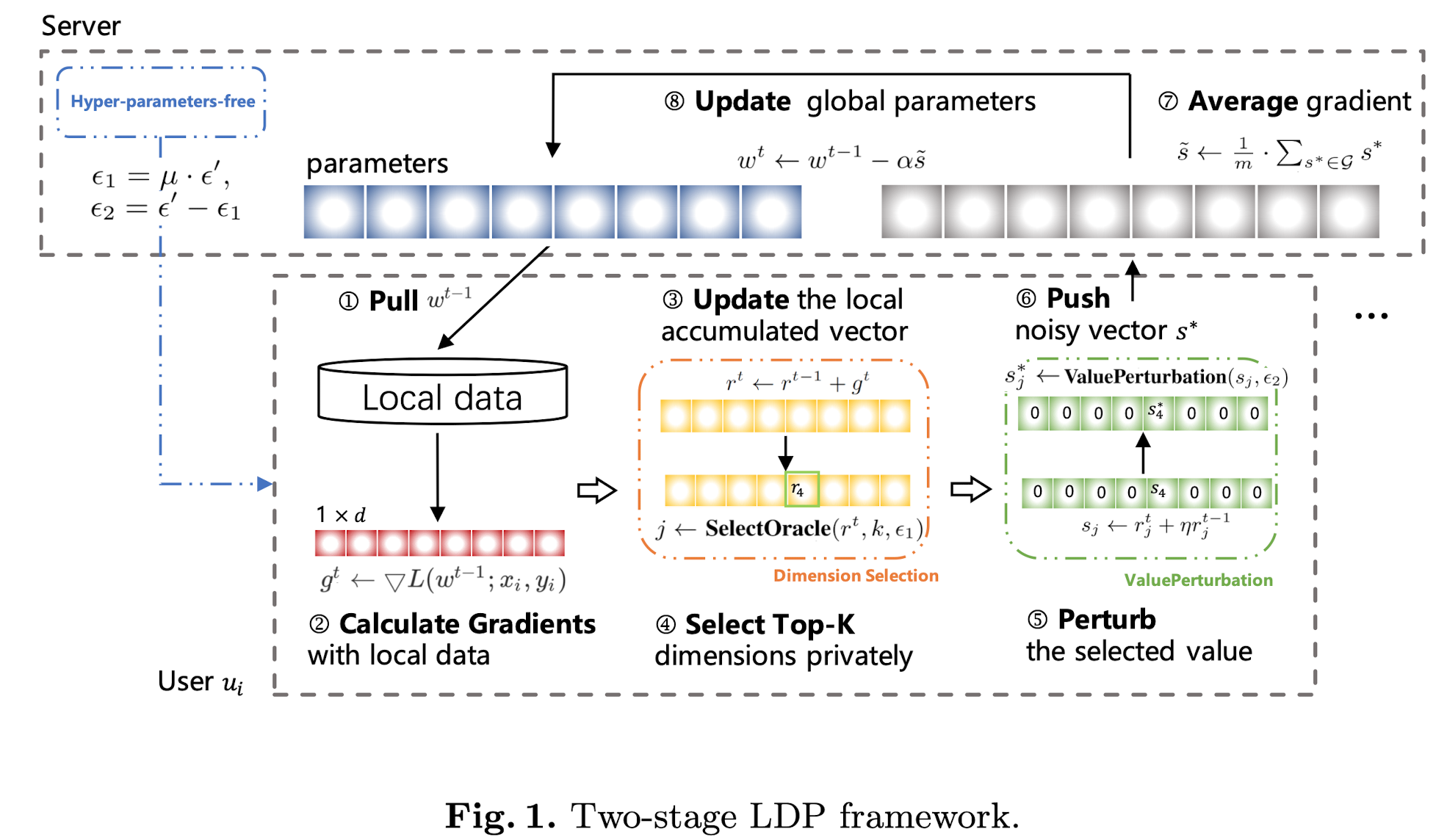
如图1所示,这一章节首先提出了一个双阶段模型:dimension selection 和 value perturbation。然后3.1节分析了和已有模型的区别,3.2分析隐私保证,3.3节进行理论分析。
Overview

首先,算法如算法1所示,我们把我们的方案和 flat solutions[13-15] 以及compressed solution[9] 相比。在我们的框架中,server首先初始化 $\mu\in[0,1]$,用于分配总的 privacy budget。对于一个 local device,其:1)将当前梯度 $g^t$ 和上一轮延迟的梯度 $r^{t-1}$累计,line15,2)用 Dimension Selection选择一个重要的维度,line16,3)对梯度进行处理,line17,然后对值进行替代,line18。line17中的操作是引入了[19]。
comparison with existing work。和已有工作最大的区别是本工作选择了一个最重要的维度。flat solution中一般随机从 $d$ 维数据中选择一个维度的数据进行值的替代。和Compressed 方法相比也有不同。
Privacy Guarantee
算法1中,accumulated vector $r$ 和 vector with momentum $s$ 都是从private data中计算的真实值,我们用 $v$ 来表示 $s$。由于本地的梯度是多维的,因此我们从隐私保护的角度来说需要考虑两个点:1)选择哪个维度的数据,2)如何保护那个选择的数据。我们用一个向量 $z\in\{0,1\}^d$ 表示top-k的ground-truth,举个例子,假如有五个维度的数据,梯度是 $[1.1,3.2,0.4,2.1,0.8]$,那么top-2对应的 $z$ 就是 $[0,1,0,1,0]$。为了保护所以有了以下两个定义:
Definition 2. 一个 dimension selection 机制 $\mathcal{M}_1$ 是 $\epsilon_1$-LDP 的,如果对于 $z,z’\in\{0,1\}^d$ 和输出 $j\in[d]$,有 $\Pr[\mathcal{M}_1(z)=j]\le e^\epsilon \cdot\Pr[\mathcal{M}_1(z’)=j]$
Definition 3. 一个 value perturbation 机制 $\mathcal{M}_2$ 是 $\epsilon_2$-LDP 的,如果对于输入 $v_j,v_j’$ 和输出 $v_j^*$ 有:$\Pr[\mathcal{M}_2(v_j)=v_j^*]\le e^\epsilon \cdot\Pr[\mathcal{M}_2(v_j’)=v_j^*]$
同样,这里也有组合性质,即定理1所描述的:
Theorem 1:对于local vector $v$,如果two-stage机制 $\mathcal{M}$ 首先由 $\mathcal{M}_1$ 选取维度 $j$,然后由 $\mathcal{M}_2$ 对 $v_j$ 替代,那么 $\mathcal{M}$ 是 $(\epsilon_1+\epsilon_2)$-LDP 的。
证明过程如下:
Variance Analysis for Accumulation
已有的非隐私保护的gradients accumulation [19,21,24,25] 中,本地向量更新为 $r^t=r^{t-1}+\alpha g^t$,我们将其改为了 $r^t=r^{t-1}+g^t$,旨在降低local updates的方差,使得迭代过程更稳定。
Private Dimension Selection
这一节分析维度选择的算法。
Selection Mechanisms
Exponential Mechanism (EXP):最容易想到的应该就是指数机制了。指数机制可以怎么用过来呢,对于一个用户的 accumulated vector $r$,我们先将其按照绝对值降序排列。对于第 $j$ 个维度,,我们将其的utility score 定位其排序 $\rho_j$。那么绝对值最大的就以较大的概率输出了。也就是 index $j\in[d]$ 输出的概率为:$\frac{\exp \left(\frac{\epsilon_{1} \rho_{j}}{d-1}\right)}{\sum_{i=1}^{d} \exp \left(\frac{\epsilon_{1} \rho_{i}}{d-1}\right)}$。其LDP的证明如 Lemma 1所示。
Lemma 1. EXP机制满足 $\epsilon_1$-LDP。
给定两个ranking向量,$z, z^{\prime} \in\{1, \cdots, d-1\}^{d}$,$j$ 表示输出index,在 $z,z’$ 中对应的 $j$ 的ranking是 $\rho,\rho’$,那么以下证明成立:
举个例子,假如某个用户的梯度是 $[0.3, 1.2, 0.6]$,那么其对应的utility就是 $[1,3,2]$,然后再以一定的概率输出对应项即可。
但是,指数机制的问题在于,我们有时候比较关心 top-k 的,所以作者提出了新的机制。
Perturbed Encoding Mechanism (PE):首先,我们依然需要和EXP一样的排序过程。然后我们引入一个top-k的标志位,设其为 $z$。然后我们将 randomized response 用到 $z$ 上。假设 $\hat{z}$ 是经过randomized response的,其中可能有多个1,也可能全为0。我们把为1的index集合起来令其为 $\mathbb{S}$。如果 $\mathbb{S}$ 是空集,那么客户上传一个 $\perp$,如果不是空集,那么客户从里面随机选一个并上传。其隐私保证由lemma 2给出。
有点绕,举个例子,依然假设用户数据是$[0.3, 1.2, 0.6]$,此时我么关心top-2。那么这时候的 $z=[0,1,1]$,然后我们对其用 RR,假设 $\hat{z}=[1,0,1]$,这时候我们从第一个或者第三个里面随机选一个作为index。如果 $\hat{z}=[0,0,0]$ 的话,我们就发送 $\perp$。
Lemma 2. PE 满足 $\epsilon_1$-LDP。
证明:首先我们看一下 $\hat{z}$ 中有多少个1:
给定两个向量 $z,z’\in\{0,1\}^d$,其中都有 $k$ 个非0向量。那么对于输出有两种情况,1)$\mathbb{S}$ 非空,$j\in\{1,2,…,d\}$。2)$\mathbb{S}$ 为空集,$j=\perp$。对于第一种情况,我们有:
对于第二种情况,我们有:
所以这个机制满足 $\epsilon_1$-LDP。
Perturbed Sampling Mechanism (PS)。类似于PE,作者提出了另一个机制。对于 top-k 的,我们以 $p$ 概率去index,对于不是 top-k 的,我们以 $1-p$ 去index,这里,$p=\frac{e^{\epsilon_{1} \cdot k}}{d-k+e^{\epsilon_{1} \cdot k}}$。其LDP的证明如 lemma 3所示。
Lemma 3. 给定两个top-k状态向量 $z,z’$和输出 index $j\in\{1,2,…,d\}$,下式成立:
Analyses of accuracy and time complexity
我们用 error bound 来分析给出的 two-stage framework,如定理3所示。定理3和value perturbation是无关的。在平均的梯度向量中引入的噪声大小为 $O\left(\frac{\sqrt{\log d}}{\epsilon_{2} \sqrt{m d}}\right)$,然后可接受的batch 的大小为 $|m|=\Omega\left(\frac{\log d}{d \epsilon_{2}^{2}}\right)$,可以看出 batch 的大小随着维度并非线性增加的。由于 $\epsilon_2=\epsilon’(1-\mu), \epsilon’=\epsilon/E$,那么对于 $\mu<0.5$ 的时候,有$\Omega\left(E^{2} \log d / d \epsilon^{2}\right)<\Omega\left(E^{2} d \log d / \epsilon^{2}\right)$。因此我们在保证同样的privacy budget的时候可以提高进度。
Theorem 3. 对于 $j\in[d]$,令 $\tilde{s}=\frac{1}{m} \sum_{s^{*} \in \mathcal{G}} s^{*}$,$X=\frac{1}{m} \sum_{s^{*} \in \mathcal{G}} s$ 表示真实梯度平均,则,我们以 $1-\beta$ 的概率满足:
和非隐私保护的应用场景相比较,LDP对于本地设备带来了计算开销。对于EXP方案,utility score和求和操作可以被离线初始化,排序操作的复杂度为 $O(d \log d)$,作者说了这么句话没懂 mapping all $d$ dimensions to according utility values consumes $O(d^2)$。然后sampling 复杂度为 $O(d)$,所以EXP的总的计算代价为 $O\left(d \log d+d^{2}+d\right)=O\left(d^{2}\right)$。然后对于PE是 $O(d \log d + d^2 + l)=O(d\log d)$,对于PS也是类似的。
Experiments
这里到了评估算法的时候了。
Experimental Setup
Datasets and Benchmarks. 为了控制数据稀疏度,我们首先用论文[26]中的过程生成了数据集,参数为 $C_{1}=\{0.01,0.1\}, C_{2}=\{0.6,0.9\}$,维度为 $\{100(\text { syn-L }), 300( \text { syn-H)\} }$,分别有 $\{60000, 100000\}$ 条数据。同时采用了BANK, ADULT, KDD99数据集,维度为 $\{32, 123,114\}$,数据量为 $\{45211, 48842, 70000\}$。同时测试的任务是逻辑回归和支持向量机。数据集信息我汇总如下:
| 数据集 | 维度 | 数据量 |
|---|---|---|
| syn-L | 100 | 60,000 |
| syn-H | 300 | 100,000 |
| BANK | 32 | 45,211 |
| ADULT | 123 | 48,842 |
| KDD99 | 114 | 70,000 |
Choices of Parameters. 由于我们观测到所有数据集都在100轮迭代之内收敛,我们的batch设置为 $m=0.01\cdot N$. 平均结果运行十次,采用 5-folds交叉验证。然后 discounting factor $\eta$ 和学习率 $\alpha$ 设置为一样,其他默认参数默认设置为 $k=0.1 d, \mu=0.1, \lambda=0.0001$。
Comparisons with Competitors. 表2描述了一些比较的方法

Evaluation of the Dimension Selection

Convergence and Accuracy. 图2(a-d)给出了错误分类的比例,这里没有比较第二阶段的value perturbation。
NP-K 和 NP-RS 的比较深刻地标明top-k在这一类的任务中是有效的。在图2(a)的100维的数据中,NP-K嘴和NP想接近。除此之外,$\epsilon_1=4$时,如图2(a)和(b)所示,EXP/PE/PS比NP-RS收敛更快。当privacy budget更大时,如图2(c-d)EXP/PE/PS慢慢会达到 NP-K($k=1$)同样的准确率。
Validation of Complexity Analysis. 图2(e) 比较了不同方法的效率问题。
Effectiveness of the Two-stage Framework
上面之比较了第一个阶段,这里开始比较两阶段的结果了。
Comparison with Existing Solutions. 第二个阶段引入了PM/HM/Duchi和compressed solution。结果也在图2中所示。为了更好地去比较,作者定义了一些比较,如表3所示。定义为:
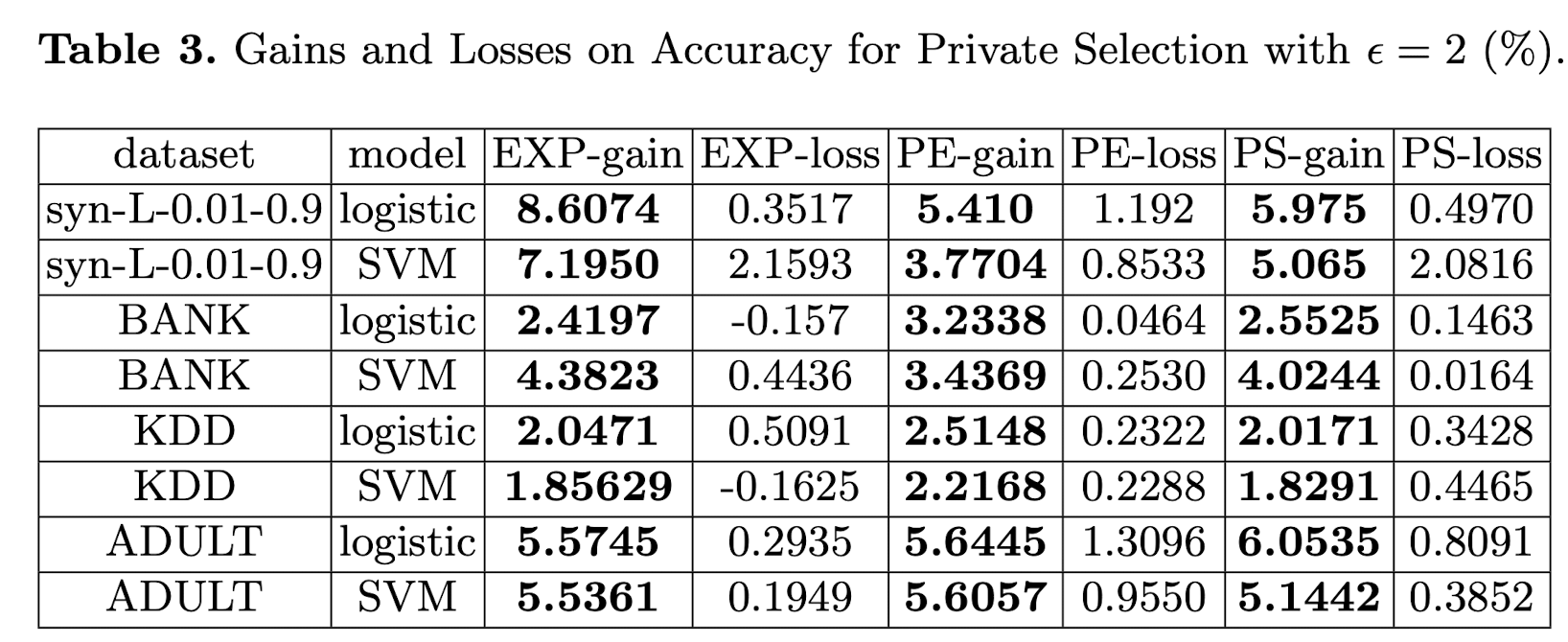
对于图2每个图的分析,可以查看原文去更细致了解。
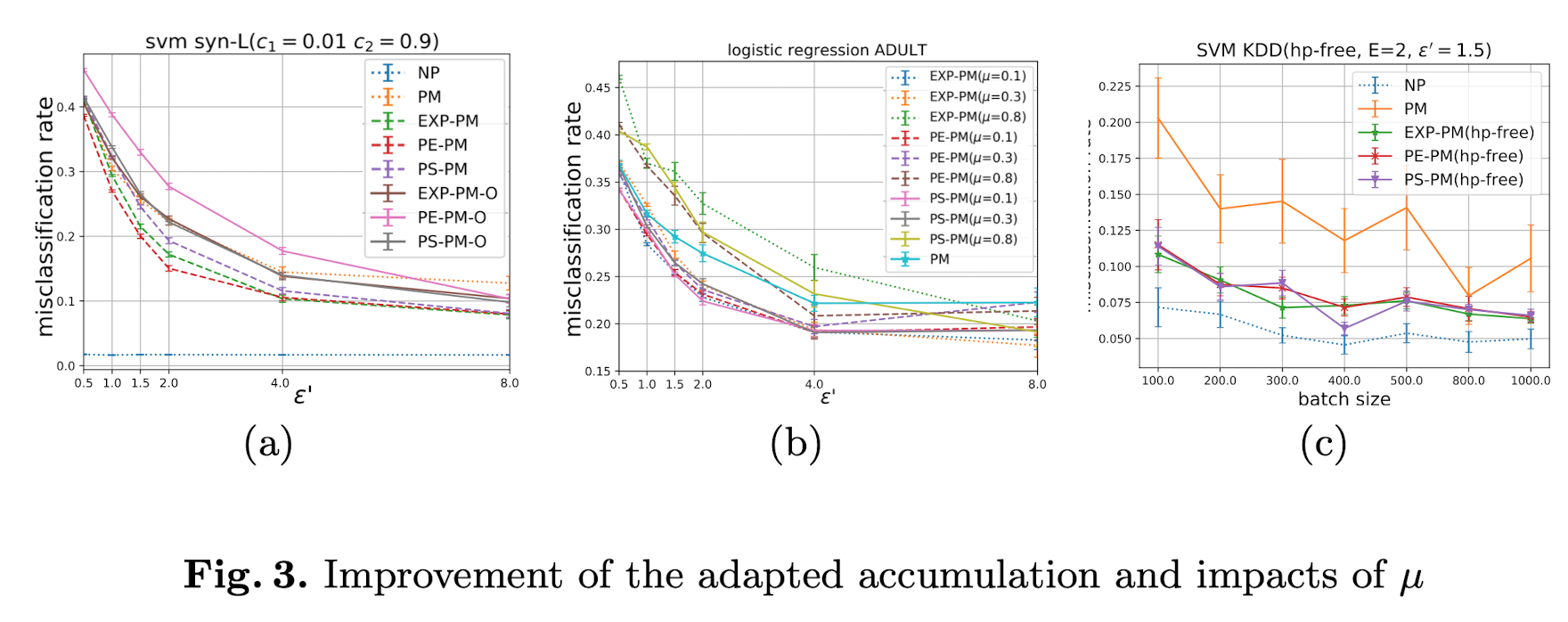
Effectiveness of the Adapted Accumulation. 图3(a)写了3.3节中的分析结果。其表明直接 accumulating $\alpha g$ 不会改进学习效果,所以我们在隐私前提的改进有一定作用。
Impacts of $\mu$. 图3(b-c)修改了两个阶段privacy budget的比例,然后查看实验结果。
Conclusions
总的来说,本文提出了一个两阶段的方案用于 federated SGD。key idea就是我们通过引入 top-k的方式来对噪声进行一定的限制。我们也改进了梯度的 accumulation 。同时理论上和实验上,我们都分析了我们方法的优点。
本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。


